Force identification
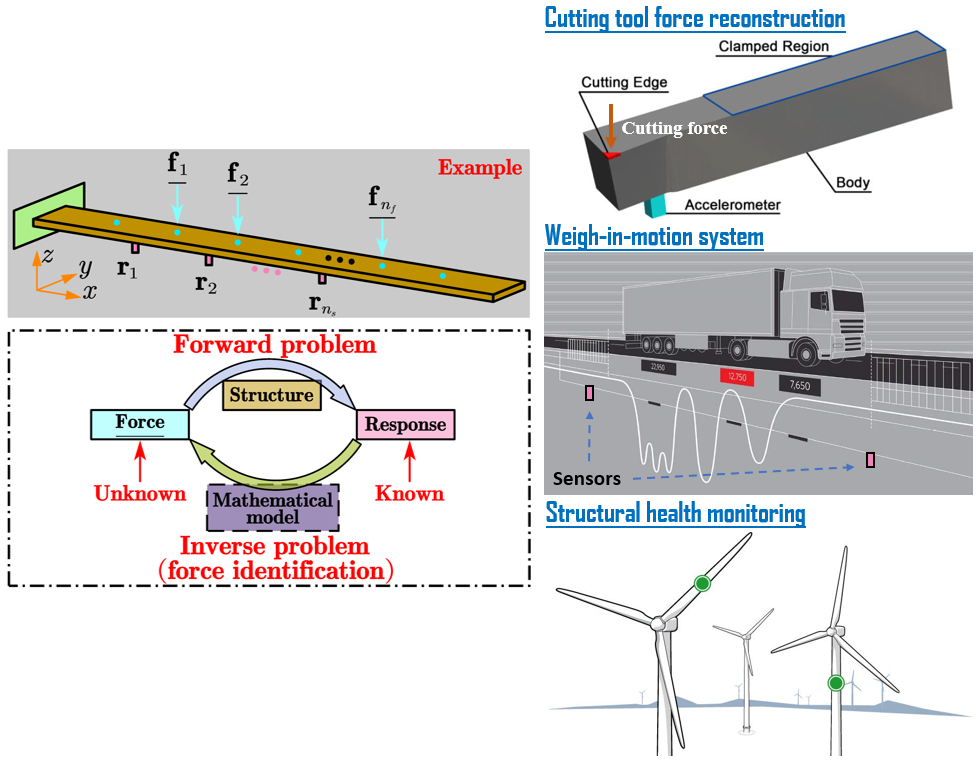
Three critical concepts exist in structural dynamics:
- Input forces;
- Structure or system;
- Output responses.
The forward problem is defined as calculating the output of a certain structure if information on input forces and structure properties is given. Identification of system parameters or model based on known input and output is called type-I inverse problem. Identification of input forces based on known system model and measured output is type-II inverse problem, the focus of this article and the theme of my Ph.D. reserach.
For linear elastic structures, the input-output mapping, i.e. the system model, is generally quite straight forward. In frequency domain, it can be represented by a frequency response function. In time domain, the mapping is characterized by a Duhamel’s intergral. In this sense, time domain inverse force identification is mathematically equivalent to solving the type II Volterra integral equation. This problem is generally ill-conditioned or ill-posed. So a majority of our efforts have been directed to developing specilized regularization techniques for this problem.
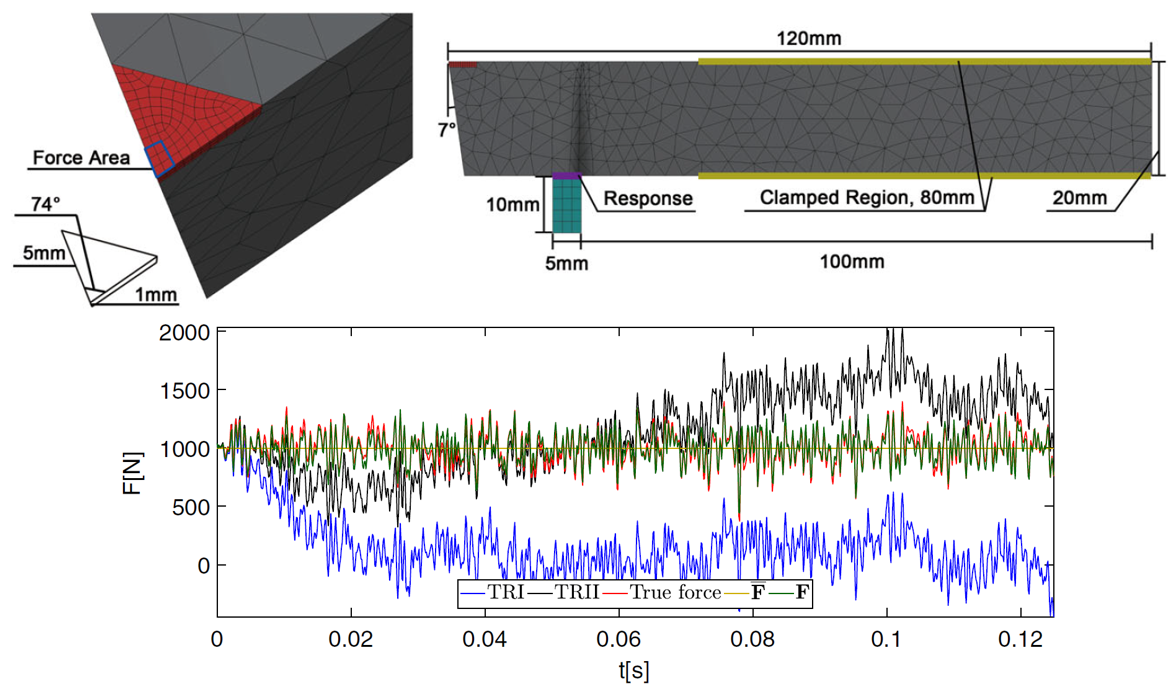
An example is the cutting tool force identification/reconsturction. The cutting tool force is typically characterized by a constant component which is the desired force value, and a dynamic component which is caused by the inevitable interaction between the working piece and the tool. To accurately identify both the constant and dynamic component, an adatpive method based on the hierarchical Bayesian framework is proposed. In this method, we separate the identification of constant and dynamic components by assigning an to-be-determined mean term to the prior distribution of unknown force history. Traditional methods, such as TRI and TRII, is mathematically equivalent to assuming a zero mean term in the prior distribution of unknown force history and cannot identify the constant component correctly. See the following figure.