Artificial intelligence for physics
ESNN: Euclidean symmetric neural network
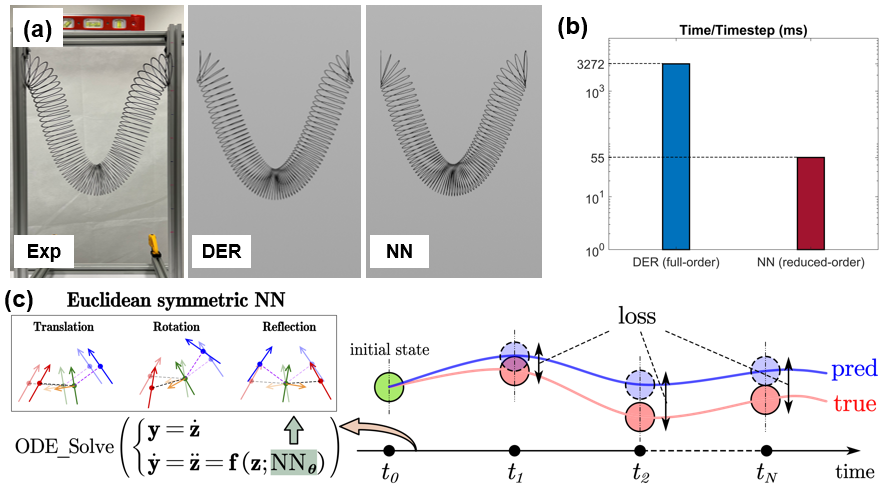
Reduced-order models (ROMs) enable the accelerated simulation of dynamic systems. However, without the guidance of physical principles, ROMs are usually hand-crafted, thus requiring tedious symbolic derivation and relying largely on engineering experience. We aim to develop a general data-driven method/pipeline for buidling ROMs while excluding the general requirement of collecting large datasets for neural network (NN) training.
ESNN is able to build accurate and generalizable ROMs (with testing on a Slinky) given a single demonstration trajectory of the system (a 76-cycle Slinky). ESNN achieves this by: 1) embedding Euclidean symmetry into its NN architecture. It first generates an Euclidean invariant (w.r.t translation, rotation, reflection) elastic energy field, and then by backpropogation induces an Euclidean equivariant conservative force field. ESNN by construction generates Euclidean equivariant elastic forces so that data augmentation (such as rotating the structure) is unnecessary; 2) training the NN under the neural ordinary differential equation (NODE) framework to match the measured trajectory. NODE, as opposed to recurrent NN which learns solutions directly, learns the derivative field, thus decoupling the initial/boundary conditions from the measured (solution) data, facilitating generalization across new initial/boundary conditions after training.
With ESNN, we were able to build an accurate ROM for a 76-cycle Slinky training with only 0.7s trajectory data. We were able to generalize the learnt model across various types of initial/boundary conditions, structure orientation, and different number of cycles. This work was highlighted on the cover of Extreme Mechanics Letters (Volume 58).
iMODE: interpretable meta neural ordinary differential equation
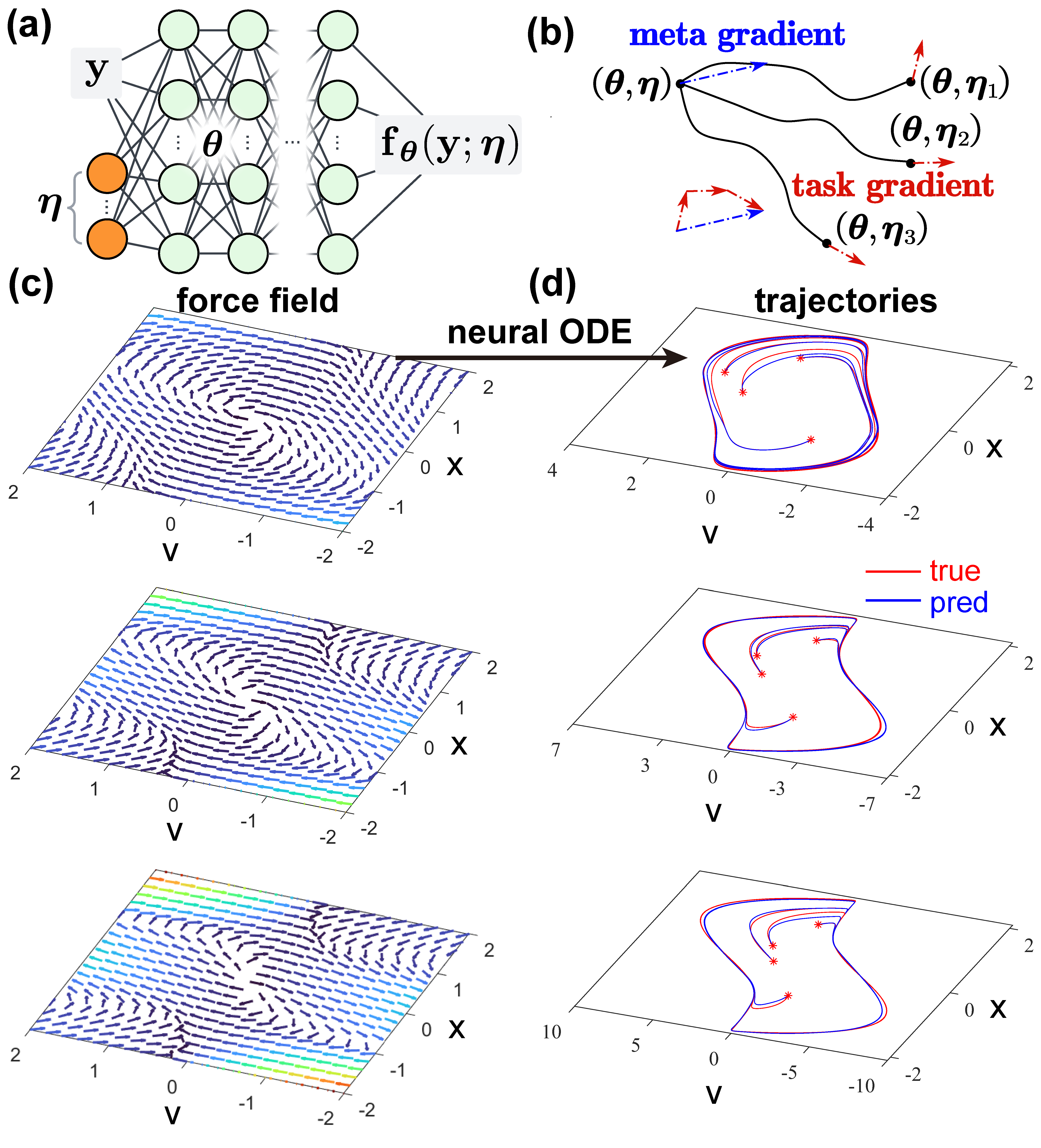
iMODE takes one step further than ESNN, with the goal of learning generalizable dynamic models for system family insteand of a system instance. A system family refers to a set of multiple system instances that share the same form of dynamics but differ in physical parameters. The essential assumption of iMODE is that the system derivative field “deforms” continuously as the physical parameter changes, and iMODE is learning such morphology, a type of meta-knowledge. If we can learn such meta-knowledge, we should be able to quickly adapt the model to any unseen system and predict its dynamics given unseen initial/boundary conditions.
Technically, iMODE constructs a NN that takes as input the system state and a concatenated latent variable, and generates as output the system derivative. The appropriate derivate field, after integrating under the NODE framework from some initial/boundary conditions, should match the ground truth trajectories; the NN weights are optimized so that after adapting the input latent variable to each individual system instance by a few (e.g. 5) steps, the adapted model becomes an accurate one for that system instance. In other words, we are finding a good NN weight so that the meta-model (with this weight) is capable of quickly adapting to system instances justified by the NODE fitting to ground truth.
iMODE is model-agnostic, i.e. the entire pipeline is capable of embedding any physical constraints, such as conserative force field, Euclidean symmetry, and so on. In fact we were able to embed the entire ESNN in iMODE, which creates a new Euclidean equivariant force field at each step when adapting the input latent variable to a new system instance. This highlights the flexibility of iMODE and its huge potential for a wide range of dynamical systems. iMODE is published on Physical Review Letters with Editors’ Suggestion and Featured in Physics.
BCRNN: Bayesian Chemical Reaction Neural Network
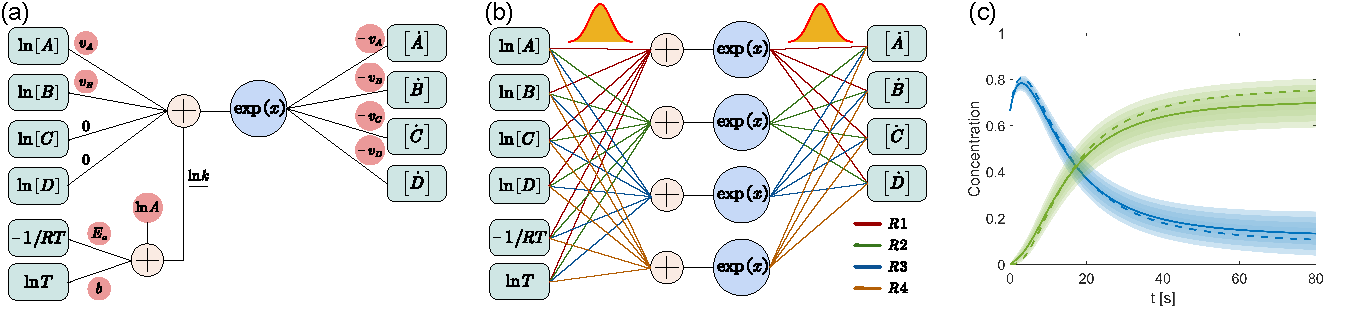
CRNN is a type of neural network (NN) that constructs a fully interpretable chemical kinetic model from a limited set of species concertration histories. It first express the widely applicable physical laws in chemical kinetics, the law of mass action and the Arrhenius law, in the form of neural networks with species concentration as inputs and species reaction rates as output; then integrates the NN under the neural ODE framework to compute predicted concentration histories; the neural network weights are updated by backpropogating the difference between predicted and measured concentration histories. This pipeline enables (1) template-free kinetic model discovery since the pathways are automatically determined in a data-driven manner instead of designated; (2) full interpretability of the NN weights as they exactly represent the stoichiometric coefficients and rate constants.
BCRNN takes one step further by assuming independent Gaussian distributions on the NN weights instead of treating them as deterministic values. In BCRNN, the number of undetermined parameters is doubled compared with CRNN: the mean and variance of the Gaussian distribution should be determined for each weight. We adopted variance inference to determine these values which eventually results in a competetion between two counteracting terms: any sampled kinetic model should predict concentration histories reasonablly close to the measured ones by the standards of the measurement noise distribution; the varainces should be reasonally small justified by the variances of the prior distribution.
After training the BCRNN, the distribution of each weight is fully determined. One can easily sample the NN weights (since they are Gaussian distributions) to construct an ensemble of kinetic models. Parallel computing on GPUs with this ensemble would enable fast kinetic prediction and uncertainty quantification under unseen conditions.
